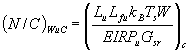 (3)
(3)
| ASSI Online | Number 1, August 1999 |
Susi Andriani, Agus B. Tjahjono, Hendri Lucky, Cessy Karina, Klaus G.
Johannsen
PSN, ASSI (Asosiasi Satelit Indonesia)
In this paper closed-form expressions are derived for the system capacity of CDMA and FDMA multiple access methods with application to multiple beam satellites.
The mobile satellite communication system under discussion operates in C-band for transmission between satellite and gateway stations (feeder link) and in L-band between the satellite and the mobile user, where a 4 MHz band has been made available (example), for Mobile Satellite Services (MSS) and for coverage over Asia.
The total L-band beam coverage is divided into spot beams and beam clusters, in each of which a part of the 4 MHz band is used or reused. If there are y spot beams and n beams / cluster, where a beam cluster may consist of 1, 4, 5 or 7 beams, then there are FR = y/n frequency spectrum reuses possible and a total effective bandwidth of 4 x FR MHz is available for transmission.
In both CDMA and FDMA the voice is vocoded, producing a bit-rate of 2.4 to 4.8 kb/s. The forward error correction (FEC) may differ for the two multiple-access system schemes. While in CDMA one can afford to apply a high-power error combatant or a very low-rate FEC code, since it does not widen the bandwidth of the pseudo-noise modulated carriers, the same kind of signal protection would increase each carrier bandwidth and therefore reduce the effective L-band bandwidth utilization in FDMA. On the other hand, while CDMA may be bandwidth efficient in L-band, the opposite is true in C-band, where a large amount of bandwidth is required to effect the C-band to L-band beam translation.
CDMA is more insensitive to fading than FDMA as long as reflected signals are delayed relative to the direct signal path by more than a chip period. Because of the natural fading protection and the superior Forward Error Correction (FEC) potential, CDMA starts out with a much lower Eb/No requirement than FDMA, and the results below have to be understood in this context.
The capacity of the satellite communications system depends on signal design, satellite antenna configuration, earth-station G/T and the fading environment. In order to develop an expression for the capacity of the satellite link, we start with a single fixed-beam antenna system and then modify the equations for multiple-beam systems.
2.0. CDMA LINK
The vocoded voice channel of 2.4 kb/s or 4.8 kb/s is error protected by a rate of 1/3 or 1/2 FEC code. The vocoded and FEC coded voice signal modulates a PN-code of 3 600 000 chips per second, which in turn Phase-Shift Keys (PSK) the RF-carrier. The spectrum of the PSK modulated carrier fits into a 4 MHz band. In case of QPSK modulation two QPSK carriers can share the 4 MHz band. The required signal energy/noise density ratio of the FEC coded voice channel, including instrumentation losses, at a bit error rate of 10-3 is 3.2 dB for rate 1/3 and 5 dB for 1/2 rate FEC.
2.1. CDMA Single Antenna Beam
The total noise/desired carrier ratio in CDMA is
( N / C ) T = ( N / C ) u + ( N / C ) d
+ ( N / C ) IM + ( N / C ) j + ( N / C ) f
(1)
where (N/C)u is the up-link noise/carrier ratio, (N/C)d the down-link noise/carrier ratio, (N/C)IM the intermodulation noise/carrier ratio, (N/C)j the noise/carrier ratio due to self-jamming and (N/C)f the noise/carrier ratio due to multipath fading.
The total noise/desired carrier ratio can be related to the processing
gain WT by setting
( N / C ) T = ( No / E b ) T
WT (2)
where (No)T is the total noise density, Eb the bit energy, W the spread bandwidth and T the information bit period.
The C-band up-link noise/carrier ratio in bandwidth W is
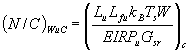 (3)
(3)
where EIRPu is the up-link EIRP, Gsr the satellite receive antenna gain, Lu the up-link path loss plus polarization loss, Lfu the fading loss of the up-link, kB Boltzmann's constant, Ts the satellite system noise temperature and W the spread spectrum bandwidth.
The L-band down-link noise/carrier ratio in bandwidth W is
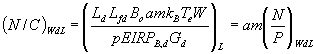 (4)
(4)
P = pEIRP B,D G d / L d L fd B o , N = kB Te W (4a)
where EIRPB,d is the satellite edge of coverage EIRP (down-link) into area B, Gd the receiving earth-station (down-link) antenna gain, Ld the down-link path loss plus polarization loss, Lfd the fading loss due to obstruction in the down-link, Bo the muticarrier back-off of the satellite power amplifier, a the voice activation (0.4), Te the earth-station system noise temperature, p is a power control improvement factor, m the number of carriers, P is total received transponder power in bandwidth W, and N is the noisepower in bandwidth W.
The system self-jamming noise/carrier ratio is
( N / C ) j = am - 1 (5)
The system self-interference or jamming is due to the presence of the other friendly but undesired active signals in the same frequency band.
The intermodulation noise will be defined by
![]() (6)
(6)
where NPR is the carrier/IM noise or noise power ratio in limiting amplifiers, which is a function of back-off and depends on the type of device and whether the device is preceded by a linearizer. The NPR is characterized by a vth law, where NPR @ 10 Bov.
The noise due to Ricean fading is considered to be caused by reflections of the desired signal and undesired signals. Assuming that a fraction 1/k of the down-link signals are reflected, then
( N / C ) f = am / k (7)
Inserting equations (2)-(7) into equation (1) and solving for m yields the CDMA channel capacity in bandwidth W :
For CDMA, single beam
m (CDMA single beam) = 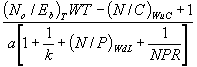 (8)
(8)
For QPSK the spread bandwidth is W/2 and the uplink noise to carrier ratio reduces also by 2, but the downlink C/N remains constant. The capacity derived for PSK remains the same for QPSK for constant bandwidth W.
m PSK = 2m QPSK = constant
Figure 1(a) illustrates how CDMA signal spectra are superimposed, which may explain the self-jamming feature of the system and how the IM noise is spread across the band.
2.2. CDMA spot-beam system
In addition to the noise sources identified in equation (1), there is interference due to spot-beam sidelobes, due to the quantization noise of the satellite processor, and due to adjacent channel crosstalk.
( N / C ) T = ( N / C ) u + ( N / C ) d + ( N / C ) IM + ( N / C ) j + ( N / C ) f + ( N / C ) sl = ( N / C ) q + ( N / C ) adj (9)
where the extra term (N/C)sl is the noise/carrier ratio due to sidelobe interference, (N/C)q is the noise to carrier ratio due to processor quantization noise and (N/C)adj is the noise to carrier ratio due to channel stacking in the feederlink. For equal user population distribution across all beam footprints, and assuming an antenna beam with spot beam area b, the number of superimposed channels seen by a particular user out of the total of M users is
![]() (10)
(10)
where B is the total scanned area. The noise/carrier ratio due to self-jamming is
( N / C ) j = ( Mab / B ) u - 1 (11)
The noise/carrier ratio due to Rician fading is
( N / C ) j = Mk / B (12)
The intermodulation noise/carrier ratio is derived by postulating that the sum signal power of M signals to IM noise ratio is equal to MC/IM, and that signals and IM noise are equally distributed among the B/b beams. Thus
![]()
and the single carrier to IM noise ratio is
![]()
( N / C ) IM = ( Mab / B (NPR)
(13)
where d is a C/IM improvement factor due to IM dispersion. The formulation implies that IM noise is distributed among the beams (see also section 3.2).
As the number of spot beams increases, the available satellite RF-power is divided among the beams. The spot beam antenna gain increases by B/b. Therefore, the aggregate EIRP into the narrow beam coverage area has increased by B/b :
EIRP b,d = (B/b) EIRP B,d
The down-link noise/carrier ratio is as given by equation (4), but with m replaced by M and the down-link wide area coverage EIRP B,d replaced by the spot beam EIRP b,d.
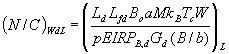 (14)
(14)
Satellite onboard processor noise
Today's mobile satellites have onboard processors which connect an uplink band to a downlink beam. Processors use A/D conversion and digital filtering. The A/D converters quantize the signal and produce quantisation noise. The combined signal to quantization noise ratio is
( N / C ) q = ( L 2 - 1 ) / p 2 pa
p2pa is a peak to average factor and L is the number of quantization levels. For noise type signals p2pa is typically 10 to 13 dB. The single channel quantization noise to carrier ratio
is ![]() (14a)
(14a)
Adjacent Channel Interference
Adjacent channel interference is due to channel stacking in the feederlink.
With m channels per frequency bin
![]() (14b)
(14b)
Sidelobe Interference
The interference suffered from sidelobe radiation of all surrounding
beams is
( N / C ) sl = Asl ( m + ( N / C ) q
+ ( N / C ) adj + ( N / C ) IM )
(15)
where Asl is a sidelobe array factor which depends on the
beam arrangement.
Figure 2 illustrates how signals are distributed over the coverage area and how signals and IM noise are divided among the various beams, which is reflected in equations (10)-(13).
Figure 3 shows two types of two-dimensional beam arrays, the honeycomb array, where six beams surround the central beam, and the square beam array where eight beams are adjacent to the central beam. In addition there is also the 4 and 7 beam cluster where the frequency band is divided among the beams within the cluster. The beam arrays shown in Figure 3 have fixed beams, with beam crossover at the 3 dB beamwidth points.
For an even user distribution, satellite beams are also evenly distributed, and overlapping. The individual user obtains a proportion b/BaM of the available broad-beam EIRP or 1/aM of the available spot beam EIRP, but also receives a proportion of the sidelobe energy.
In order to clarify this point, we first assume that each beam uses the full available frequency band and that the beams are arranged in the array shown in Figure 3(a), that (b/B)M users within each elemental beam area are located at the centre of the beam (to obtain peak EIRP) and that sidelobe interference is spilled from the surrounding beams into the central beam area. We define the sidelobe array factor as
![]() (16)
(16)
where Gsl is the equivalent composite sidelobe gain of all sidelobes falling into the intended beam area, G(0) is the peak main lobe gain, and Gsl,n is the sidelobe gain of beam n. For the circular beam array of Figure 3(a),
![]()
The beam coverage area b has the angular semidiameter F 1
= q 3dB/2. For constant antenna illumination q 3ddB
= 1.07 l /D, where l is the wavelength and D is the antenna diameter. Beams
overlap at F 1 and touch at F 2, where F 2
= 0.87 F 1. The antenna gain pattern is assumed to be :
G (z) = ( 2J1 (z) / z ) 2 = [ L1(z)
] 2 (17)
z = ( pD / l
) sin f
where J1(z) is the first order Bessel function, L 1(z) is the first order Lambda function, and z is the normalized off axis angle.
At the centre of the inner beam area the normalized off-axis angle for
one of the outer beams is z = (p D/l ) sin (2F 2) = 2.92, at
which point G (2.92) = 0.06. Therefore the normalized composite sidelobe
power is
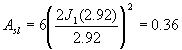
If a second ring of beams surrounds the inner beam, the sidelobe power increases to 0.46; Asl may ultimately reach the value 0.5.
For equal user distribution the sum of interference noise components due to self jamming, intermodulation, fading and quantization from signals within the intended beam, and those due to signals from other beams injected by sidelobe radiation, is such that the internal beam noise is multiplied by the factor (1 + Asl).
The term
A sb = ( 1 + Asl )(18)
is the spot beam array factor. For the beam arrangement shown in Figure 3(a) the array factor is about 1.49; and the user being located at the beam center. For a user at the 3 dB crossover the interference due to the other mobile users is about 3.5 times relative to that in a single beam, therefore Asb = 4.5.
Substituting equations (11)-(15), (17) and (18) in equation (9) where IM noise is distributed among the beams and solving for the total system capacity M yields for B/b times frequency reuse
M (CDMA forward multiple beams)
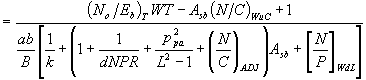 (19)
(19)
where Asb is defined by (18), its value ranging between 1.5 and 4.5.
For a multiple beam CDMA system all carriers are distributed among a fixed number of beams. At the 3 dB point of the intended beam coverage, the desired energy is reduced by as much as 3 dB, and the undesired energy for optimum beam-stacking is three times higher than that contained in a single beam.
The down-link carrier /noise ratio contains the parameter p which is a signal enhancement factor due to power control. The noise enhancement due to vehicle position and L-band down-link fading can be compensated by power control. While it is difficult in a dynamic environment to compensate for fade or obstruction loss while the mobile user is moving, one may reduce the noise enhancement due to vehicle position by increasing the C-band up-link carrier power. The power of all the vehicle-assigned carriers within a beam may be adjusted such that the EIRP is constant across the beam. This is identical to determining the average antenna gain below maximum spot beam gain, where the average is taken over the 3 dB beamwidth.
The average gain below the maximum gain within the 3 dB beam contour is
Gb = ( 4/Z12 ) I (Z1) (19a)
where I (Z1) = I - Jo2 (Z1) - J12 (Z1) (19b)
is the beam power within the 3 dB beamwidth (2 Z1), and where Jo (Z1) and J1 (Z1) are the zero order and first order Bessel functions respectively.
For Z1 = 1.027 p / 2 = 1.61 ,
the beam power is I(Z)1 = 0.47
2.3. Beam Clusters
If the frequency spectrum is divided into n parts and if each part is given a separate beam (n beam cluster), then WT reduces by n, but (N/C)u, (N/C)d and (N/C)IM also reduce by the same amount. Beam clusters for four and seven beams are shown in Figure 4.
The sidelobe power falling into a beam belonging to a beam cluster depends on the number of surrounding beams of equal frequency. For the case of 1, 4 and 7 beam clusters the sidelobe interference suffered by a mobile user located in the center of his beam is calculated in Table 1.
Table 1. Sidelobe interference with frequency reuse, mobile user
in beam center
|
|
|
||
|
|
|
|
|
| Distance between interfering beams (2f 2) of first ring |
|
|
|
| z (first ring) |
|
|
|
| L (z)2 |
|
|
|
| Nr of interefering beams, first ring |
|
|
|
| Nr x L (z)2, first ring |
|
|
|
| Distance between interfering beams of second ring |
|
|
|
| z (second ring) |
|
|
|
| L (z)2 |
|
|
|
| Nr of interfering beams, second ring |
|
|
|
| Nr x L (z)2, second ring |
|
|
|
| Total sidelobe power |
|
|
|
| Sidelobe power below peak, dB |
|
|
|
| Beam array factor, Asb |
|
|
|
Inserting all noise/carrier ratios into equation (9), one obtains for the system capacity of the forward link of the multi beam CDMA system the expression.
M (CDMA forward, clustered beams)
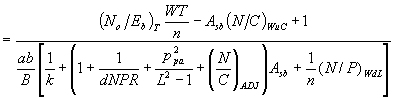 (20)
(20)
where Asb is the beam array factor. For a 4 beam cluster Asb = 1.08 and for a 7 beam cluster Asb = 1.023.
The return link from the mobile user to the gateway station suffers from the fact that the mobile user has limited EIRP. The signal is picked up by the multiple beam high gain satellite receive antenna. It undergoes processing in which L-band beam bands are translated into a C-band downlink spectrum, then it is turned over to the C-band transmitter.
The return link has several adverse effects : the up-link fade translates into a down-link fade, and the IM is not dispersed as in the forward link. Besides the low uplink CNR causes the uplink noise to take a share (1-r) of the C-band downlink EIRP. With this in mind, the return-link channel capacity can be written as
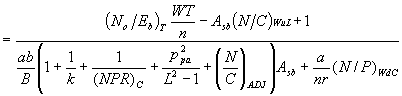 (21)
(21)
CDMA Bandwidth Utilization
Whereas CDMA uses L-bandwidth rather efficiently, it is wasteful in the feederlink bandwidth. In order to translate 4 MHz to 140 beams, 140 x 4 = 560 MHz feederlink bandwidth would be required. For clustered beams, and using a 4 beam cluster, where each beam uses 1 MHz, still 140 MHz are necessary.
NEXT:
3.0. FDMA LINK